Сначала запишем условие производственной задачи из предыдущей главы:

Ресурс	Изделие A	Изделие B	Сколько ресурса на складах
R1	1	3	15
R2	2	1	20
R3	3	2	35
Прибыль	5	10

А теперь попробуем записать систему ограничений нашей задачи и целевую функцию в виде неравенств. Обозначим за xA,xBxA,xB количество производимых изделий A и B, соответственно.

• Сколько всего потребуется ресурса R1? Для изделия A необходима 1 единица данного ресурса, а для изделия B — 3 единицы. Всего, следовательно, необходимо 1⋅xA+3⋅xB1⋅xA+3⋅xB единиц. Так как у нас 15 единиц данного ресурса на складе, необходимо, чтобы это значение было не больше чем 15: 1⋅xA+3⋅xB≤151⋅xA+3⋅xB≤15
• Сколько всего потребуется ресурса R2? Для изделия A необходимы 2 единицы данного ресурса, а для изделия B — 1 единица. Всего, следовательно, необходимо 2⋅xA+1⋅xB2⋅xA+1⋅xB единиц. Так как у нас 20 единиц данного ресурса на складе, необходимо, чтобы это значение было не больше чем 20: 2⋅xA+1⋅xB≤202⋅xA+1⋅xB≤20
• Сколько всего потребуется ресурса R3? Для изделия A необходимы 3 единицы данного ресурса, а для изделия B — 2 единицы. Всего, следовательно, необходимо 3⋅xA+2⋅xB3⋅xA+2⋅xB единиц. Так как у нас 35 единиц данного ресурса на складе, необходимо, чтобы это значение было не больше чем 35: 3⋅xA+2⋅xB≤353⋅xA+2⋅xB≤35
• Мы не можем производить отрицательное количество изделий. Следовательно, xA,xB≥0xA,xB≥0
• В итоге мы получаем 5 единиц прибыли за каждое изделие A и 10 единиц за каждое изделие B. Всего мы получаем прибыли 5⋅xA+10⋅xB5⋅xA+10⋅xB. Естественно, мы хотим максимизировать данную величину. Можно записать, что F(xA,xB)=5⋅xA+10⋅xB→maxF(xA,xB)=5⋅xA+10⋅xB→max

 

Итак, у нас получилась система ограничений и целевая функция следующего вида:

Чтобы решить данную задачу линейного программирования графическим методом, необходимо сначала превратить (мысленно) все неравенства в равенства, и на время забыть про целевую функцию. То есть, получить следующую систему:

Мы получили пять уравнений с двумя переменными, следовательно, мы можем построить их графики. Например, мы можем направить ось с переменной xAxA вправо (где обычно у нас ось абсцисс) и ось с переменной xBxB вверх (где обычно у нас ось ординат). Для построения графиков нужно лишь выразить из этих уравнений xBxB. Сделаем это:

Прежде чем строить графики, разберемся с последними двумя уравнениями, xA=0xA=0и xB=0xB=0. Эти уравнения выражают сами оси — абсцисс и ординат. А так как в исходных ограничениях были неравенства xA≥0xA≥0 и xB≥0xB≥0, то точка нашего решения должна быть правее и выше, чем эти оси — то есть, находиться в первой четверти. Поэтому эти две линии можно не строить, а просто учитывать, что решение в первой четверти.

Остальные линии мы построим на графике, и получим следующую картину (естественно, на нормальном графике не нужно рисовать такие стрелки, они лишь для наглядности, чтобы не перепутать линии друг с другом):

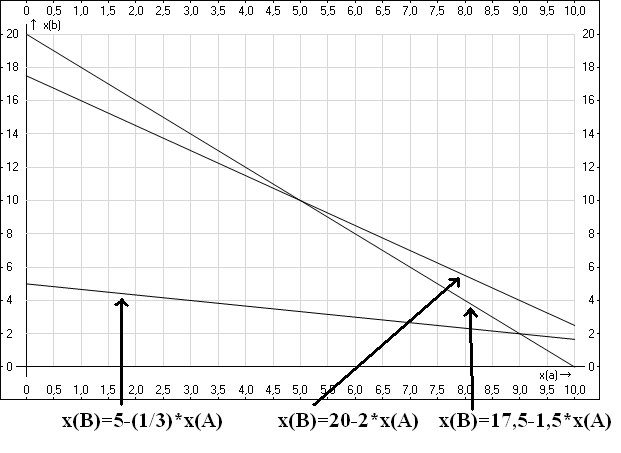
Каждая из этих линий разбивает область допустимых решений на две — одна находится правее и выше каждой из этих линий, вторая — левее и ниже. Какая из них нужна нам? Та, которая левее и ниже. Во-первых, в исходных неравенствах у нас был знак «меньше или равно», а левее и ниже как раз более маленькие значения переменных. А во-вторых, как мы говорили в предыдущем пункте, решение (0,0) вполне удовлетворяет условию задачи, хоть и не является оптимальным. А точка (0,0) — начало координат — расположена как раз левее и ниже каждой из прямых.

То есть, нам нужно найти область, расположенную левее и ниже, чем каждая из наших прямых. Отобразим ее:

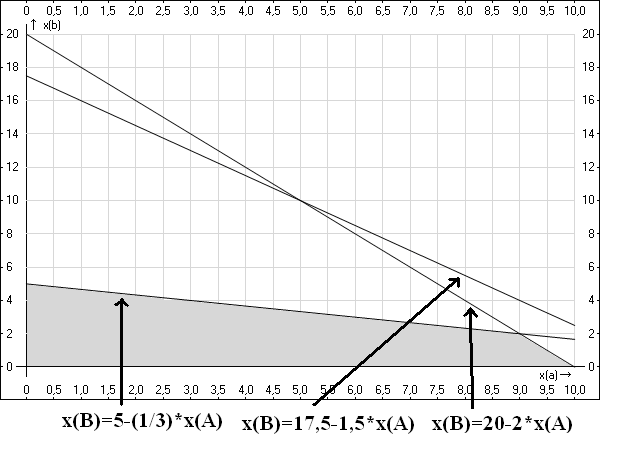
Эта область, во-первых, расположена в первой четверти, как и должно быть, во-вторых, левее и ниже прямых xB=5−13xAxB=5−13xA и xB=20−2xAxB=20−2xA. Прямая xB=17,5−1,5xAxB=17,5−1,5xA оказалась не участвующей в решении, так иногда бывает, это не страшно.

Далее задачу можно решать двумя способами.

Основной способ

Рассмотрим первый из них. Для него нужно нарисовать линию нулевого дохода, то есть, линию, при которой целевая функция равна нулю: 5xA+10xB=05xA+10xB=0. Если упростить данное выражение, получим xB=−0,5xAxB=−0,5xA. Построим эту функцию красным цветом, и уберем подписи. Она будет расположена не в первой четверти, это нормально.

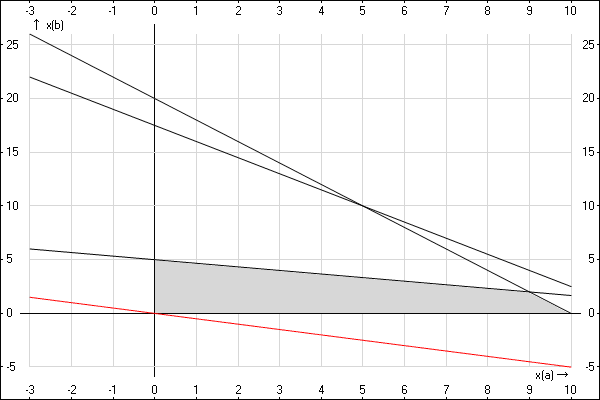
Эта линия состоит из точек, каждая из которых является решением, применяя которое, мы получим нулевой доход. Однако с тем условием, что xA,xB≥0xA,xB≥0, такое решение мы получаем всего одно — в точке (0,0) — остальные точки лежат во второй и четвертой четверти.

Что будет, если эту линию поднимать выше (параллельным переносом)? Мы получим линии, которые будут давать больший, чем 0 доход. Получается, чем выше мы поднимем данную линию, тем лучше. Однако совсем до бесконечности поднимать ее не получится, ведь она должна хотя бы касаться разрешенной области, обозначенной серым цветом (сейчас она касается только в точке (0,0)). Попробуем провести (пока на глаз) линии, параллельные данной, через оставшиеся три точки многоугольника:

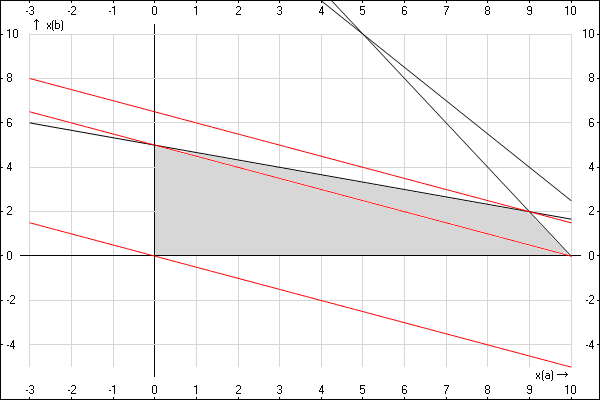
Мы нарисовали еще две линии, параллельные линии нулевого дохода, но расположенные выше. Средняя из них проходит через две точки нашего многоугольника с решениями, а самая высокая — через еще одну точку многоугольника. Кроме того, она вообще пересекает наш многоугольник в одной-единственной точке. И еще выше данную линию поднять нельзя — она вообще перестанет пересекать наш многоугольник. Следовательно, эта линия и есть «линия максимального дохода», а наше решение находится, как раз, в той точке, в которой эта линия пересекает нашу область допустимых решений — в точке пересечения линий xB=5−13xAxB=5−13xA и xB=20−2xAxB=20−2xA. Найдем координаты данной точки. Для этого приравняем эти два значения для xBxB:

Итак, наше решение находится в точке (9,2). Это означает, что необходимо производить 9 единиц изделия A и 2 единицы изделия B. При этом мы получим прибыль

Во всех остальных точках многоугольника решений прибыль будет меньше.

Другой способ

Второй способ заключается в том, что нужно просто проверить значение целевой функции в каждой точке многоугольника. Всего их четыре. Обозначим их буквами:

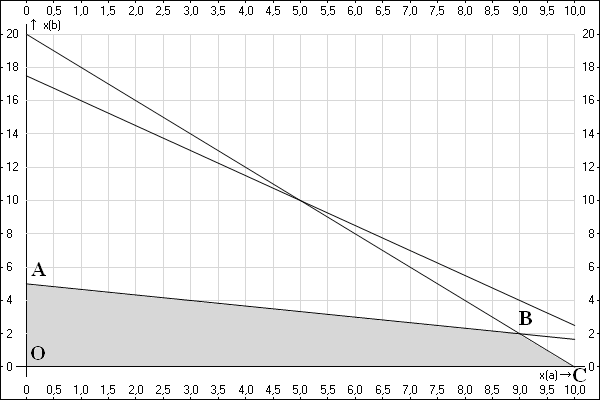
Найдем координаты каждой из них. Координаты точки O мы знаем — (0,0). Координаты точки B мы нашли выше (по первому способу) — (9,2). Точка A — это точка на прямой xB=5−13xAxB=5−13xA, причем xA=0xA=0. Следовательно xB=5xB=5. То есть, ее координаты (0,5). Точка C — это точка на прямой xB=20−2xAxB=20−2xA, причем xB=0xB=0. То есть, 20−2xA=020−2xA=0, 2xA=202xA=20, xA=10xA=10. Следовательно, ее координаты (10,0).

Теперь найдем значение целевой функции в каждой из данных точек:

Действительно, в точке B наша функция принимает максимальное значение, равное 65. Это и есть максимальная прибыль, которую можно получить в данном случае.

А если товаров больше?

Как говорилось в предыдущем разделе, графическим способом можно решать только задачу для двух производимых товаров. Это потому, что если товаров будет больше двух, то и переменных будет больше двух, например, три — xA,xB,xCxA,xB,xC. И тогда придется строить трехмерный график, в котором запросто можно запутаться. А если переменных больше трех, то график не построить вообще. Однако специально для этих случаев был разработан еще один метод решения задач линейного программирования, и, в частности, производственной задачи — симплекс-метод, который мы рассмотрим в следующей главе.